When you look at a graph, one of the simplest shapes you’ll see is a straight line. A line doesn’t curve or bend—it moves in one constant direction.

Think about real life: many situations can be represented by a straight line.

• Example 1: Taxi fare – Imagine a taxi that charges a $3 base fee, plus $2 for every mile you ride. The total cost goes up in a straight, predictable way as you travel more miles.
• Example 2: Cell phone plan – A plan might have a $10 monthly fee, plus $5 for every gigabyte of data you use. Again, the cost increases steadily.

We can describe these kinds of relationships with an equation in slope-intercept form:

y= mx + b

• m = slope → the rate of change (how quickly y increases or decreases as x changes).
  • In the taxi example, the slope is 2, because the price goes up $2 for each mile.
• b = y-intercept → the starting value, or where the line crosses the y-axis.
  • In the taxi example, the y-intercept is 3, because the ride costs $3 before you even travel a mile.

So the equation for the taxi ride would look like: y=2x+3

This means:

• Start at $3 (the y-intercept).
• Add $2 for every mile you go (the slope).

When graphed, this equation makes a straight line that shows the relationship between miles and cost.

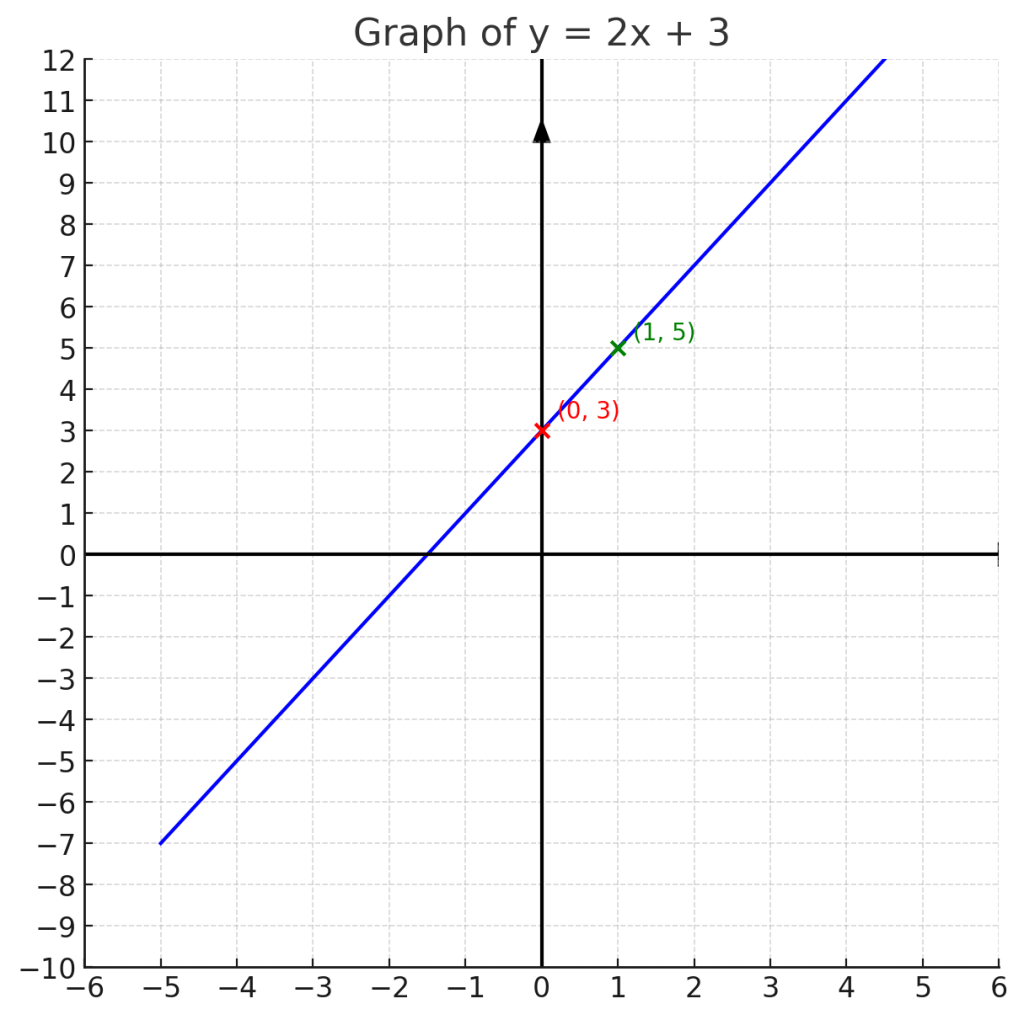
Here’s the simplified “cross method” graph of y=2x+3:

• The x-axis and y-axis cross at the origin (0,0), with arrows showing they extend in both directions.
• The red point marks the y-intercept (0,3).
• The green point shows the next step using the slope: up 2, over 1 → (1,5).
• The line passes through these points and continues infinitely.

🔑 Helpful Hints for Graphing Linear Equations

1. Always start with the y-intercept (b).
   • Look at the equation y=mx+b
   • Plot the point (0,b) on the y-axis first.
   • Example: in y=2x+3 , start at (0,3).
2. Use the slope (m) as rise/run.
   • Slope tells you how the line moves.
   • Positive slope = line goes up from left to right.
   • Negative slope = line goes down from left to right.
   • Example: slope 2 means up 2, right 1.
3. Plot at least 2 points before drawing the line.
   • After plotting the intercept, use slope to find a second point.
   • Connect them with a straight edge (ruler if possible).
4. Extend the line across the graph.
   • A line goes on forever in both directions, so draw it through your points across the whole grid.
   • Add arrows at both ends to show it keeps going.
5. Check your work.
   • Pick a value of x, plug it into the equation, and see if your point is on the line.
   • Example: In y=2x+3, if x=2 , then y=7. Does your line pass through (2,7)?

---

Example 2:

Graphing y=−x+1

1. Identify slope and intercept:
   • Equation: y=−x+1
   • Slope (m) = −1 → means down 1, right 1.
   • Intercept (b) = 1 → y-intercept is at (0,1).
2. Plot the y-intercept:
   • Start at the point (0,1) on the y-axis.
3. Use the slope:
   • From (0,1), go down 1 and right 1 to reach (1,0).
   • Plot this point too.
4. Draw the line:
   • Connect the points with a straight line.
   • Extend across the graph with arrows on both ends.

Extra Explanation:

---

What the line looks like:

• It starts at (0,1).
• It moves downward as you go right (negative slope).
• The line passes through points like (1,0), (2,−1), and (−1,2).

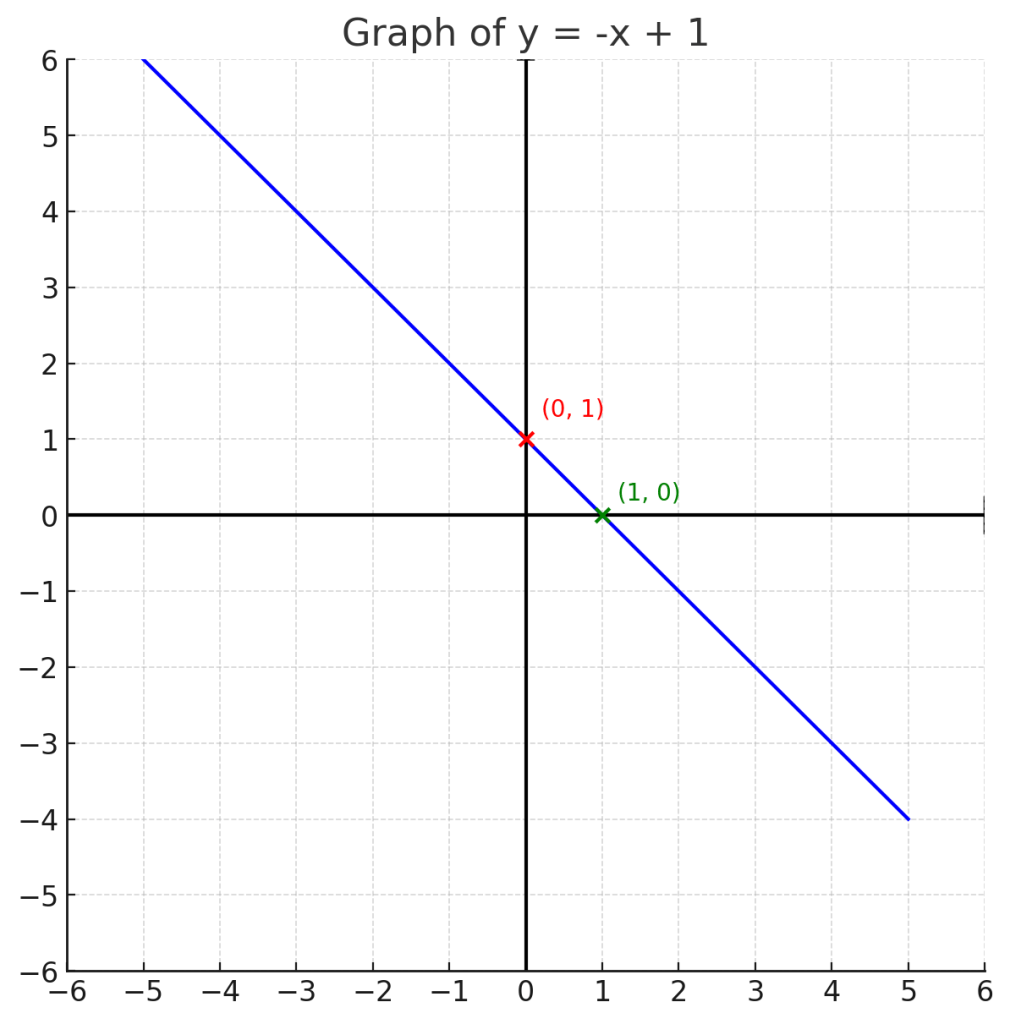
Here’s the cross-method graph of y=−x+1:

• The red point is the y-intercept (0,1).
• The green point shows the slope: from (0,1), move down 1, right 1 to reach (1,0).
• The line continues in both directions, slanting downward from left to right (negative slope).

Here’s the graph of y=−x+1 with arrows showing the rise/run method:

• From the y-intercept (0, 1), the purple arrows guide you:
  • Go down 1 (rise = -1).
  • Go right 1 (run = +1).
• This takes you to the next point (1,0).

Practice Worksheet: Slope-Intercept Form

For each equation:

1. Identify the slope (m) and y-intercept (b).
2. Plot the y-intercept on the graph.
3. Use the slope (rise/run) to find at least one more point.
4. Draw the line through the points.